



Next: Practice in DEVS++
Up: Performance Measures
Previous: Average Queue Length
Contents
Index
Sample Mean, Sample Variance, and Confidence Interval
If the internal components
of a system behave stochastically or if its input events can occur
at arbitrary times, the performance have randomness.
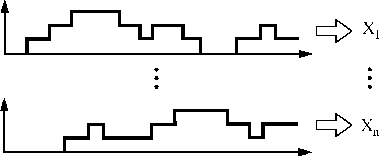
If we reset the model under study prior to each simulation run,
the performance indices from each run are independent
from those of all the other runs. Random variables are said to be
identically distributed if the associated variables have
identical measurement. For examples, the Utilization of
Processor in BufferProcessor of Figure
4.1 from multiple simulation runs are independent and
identically distributed (IID) random variable.
Figure 4.5:
IID random variants
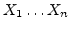 from
from 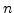 simulation
runs
simulation
runs
 |
Suppose that we try to estimate the real mean 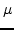 of a random
variable from a sample whose values are
of a random
variable from a sample whose values are
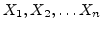 from
from 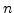 simulation runs as illustrated in Figure 4.5.
Then the sample mean
simulation runs as illustrated in Figure 4.5.
Then the sample mean
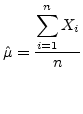 |
(5.8) |
is an unbiased (point) estimator of the real mean 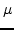 .
Similarly, the sample variance
.
Similarly, the sample variance
![$\displaystyle \hat{\sigma}^2(n)=\frac{\displaystyle{\sum_{i=1}^{n} [X_i-\hat{\mu}]^2}}{n-1}$](img149.gif) |
(5.9) |
is an unbiased estimator of the real variance 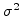 . For
. For 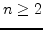 , a 100(
, a 100(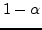 ) percent confidence interval for
) percent confidence interval for 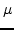 is
given by
is
given by
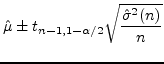 |
(5.10) |
where
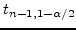 is the upper
is the upper
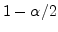 critical
point for the
critical
point for the 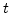 distribution with
distribution with 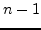 degree of freedom. It
can be written
degree of freedom. It
can be written
![$\displaystyle P\biggl[\hat{\mu}- t_{n-1,1-\alpha/2}\sqrt{\frac{\hat{\sigma}^2(n...
...hat{\mu}+ t_{n-1,1-\alpha/2}\sqrt{\frac{\hat{\sigma}^2(n)}{n}} \biggr]=1-\alpha$](img158.gif) |
(5.11) |
and we say that we are 100(1-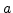 ) percent confident that the real
) percent confident that the real
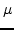 lies in the interval given by Equation
(4.10).
lies in the interval given by Equation
(4.10).
Example 5.5
Suppose that 10 simulation runs produce system throughput data
of 12.0, 15.0, 16.8, 18.9, 9.5, 14.9, 15.8, 15.5, 5.0, and 10.9.
Our objective is to build the 90 % confidence interval for
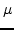
.
We have t-distribution values of
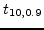
=1.372,
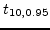
=1.812,
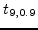
=1.383,
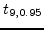
=1.833.
Then 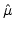 =13.4 and
=13.4 and
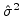 =1.7 and the 90%
confidence interval for
=1.7 and the 90%
confidence interval for 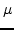 is
is
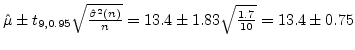

The values of
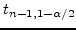 of
of 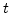 pdf are available in
many statistics books and simulation books [Zei76,LK91]. DEVS++ calculates the 100(1-
pdf are available in
many statistics books and simulation books [Zei76,LK91]. DEVS++ calculates the 100(1- ) confidence
interval for
) confidence
interval for 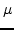 when using
when using mrun n for 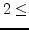
n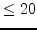 in verion 1.4.1We will see it in detail in
Section 4.3.
in verion 1.4.1We will see it in detail in
Section 4.3.




Next: Practice in DEVS++
Up: Performance Measures
Previous: Average Queue Length
Contents
Index
MHHwang
2007-05-07

![]() of a random
variable from a sample whose values are
of a random
variable from a sample whose values are
![]() from
from ![]() simulation runs as illustrated in Figure 4.5.
Then the sample mean
simulation runs as illustrated in Figure 4.5.
Then the sample mean
![$\displaystyle P\biggl[\hat{\mu}- t_{n-1,1-\alpha/2}\sqrt{\frac{\hat{\sigma}^2(n...
...hat{\mu}+ t_{n-1,1-\alpha/2}\sqrt{\frac{\hat{\sigma}^2(n)}{n}} \biggr]=1-\alpha$](img158.gif)
![]() =13.4 and
=13.4 and
![]() =1.7 and the 90%
confidence interval for
=1.7 and the 90%
confidence interval for ![]() is
is
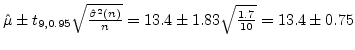
![]()
![]() of
of ![]() pdf are available in
many statistics books and simulation books [Zei76,LK91]. DEVS++ calculates the 100(1-
pdf are available in
many statistics books and simulation books [Zei76,LK91]. DEVS++ calculates the 100(1-![]() ) confidence
interval for
) confidence
interval for ![]() when using
when using ![]()
![]() in verion 1.4.1We will see it in detail in
Section 4.3.
in verion 1.4.1We will see it in detail in
Section 4.3.