- update
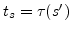 and
and 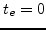 if
if
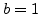 ;
;
- keep
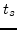 and
and 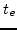 preserved if
preserved if 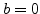 .
.
Notice that the elapsed time ![]() increases linearly over time so
it is a continuous variable whose time derivative is constant 1.
However, the lifetime
increases linearly over time so
it is a continuous variable whose time derivative is constant 1.
However, the lifetime ![]() is not changing continuously but it
is determined discretely at the time of executing either
is not changing continuously but it
is determined discretely at the time of executing either
![]() or
or ![]() .
.
In other word, suppose that there is
![]() at time
at time
![]() , there is another
, there is another
![]() at time
at time
![]() and
and
![]() . If there is no event between
. If there is no event between ![]() and
and ![]() , it implies that the only difference between
, it implies that the only difference between ![]() and
and
![]() is that their elapsed time such that
is that their elapsed time such that
![]() .
.
Formally we can rewrite this player as
![]() where
where
![]() ={
={?receive}; ![]() ={
={!send};![]() ={
={Send,
Wait}; ![]() =
=Send; ![]() (
(Send)![]() [0.1,
1.2],
[0.1,
1.2], ![]() (
(Wait)=![]() ;
;
![]() (
(Send,![]() ,[0,
,[0,![]() ],
],?receive)
=(Send,1),
![]() (
(Send,[0.1,
1.2],[0,![]() ],
],?receive)=(Send,0);
![]() (
(Send)=(!send,Wait);
![]()