Monorail System

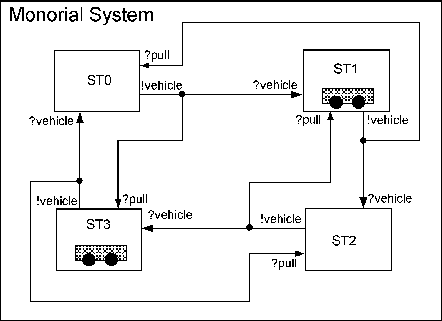
Figure 3.3 illustrates the configuration of a monorail system which consists of four stations whose names are ST0, ST1, ST2 and ST3, respectively.

Figure 3.3: Monorail System

Each station, ST0, ST1, ST2 and ST3, is an instance of Station class derived from Atomic such that it has an input event set $X$ = {?vehicle, ?pull} and an output event set $Y$ ={!vehicle, !pull} and two state variables: phase $\in$ {Empty (E), Loading (L), Sending (S), Waiting (W), Collided (C)}, and nso $\in$ {false(f), true(t)} indicating ``next station is NOT occupied'' for nso=f or ``next station is occupied'' for nso=t.

To avoid collisions that can occur when more than one vehicle attempts to occupy a station (let's call it $A$ ) at the same time, the station prior to $A$ (let's call it $B$ ) should dispatch the vehicle ONLY when $B$ 's nso = f. The phase transition diagram of a single station is shown in Figure 3.4 where an arc is augmented by (pre-condition),(post-condition). For example, when a station receives ?p at phase=E, it makes nso=f; if phase=L and nso=f, then when it receives ?p, it changes into phase=S internally without any output indicated by !$\epsilon$ . The symbols ?v, ?p, and !v in Figure 3.2 stand for ?vehicle, ?pull, and !vehicle, respectively.

The loading time $lt$ is assigned as $lt=10$ for ST0, ST2, ST3; $lt=30$ for ST1 (because ST1 is bigger than the rest other three stations). The initial state for each station is $s_0=(\verb''E'',\verb''t'')$ for ST0 and ST2, $s_0=(\verb''L'',\verb''f'')$ for ST1 and ST3.

Figure 3.4: Phase Transition Diagram of Station

To model and simulate this monorail system, we build Station as follows.